Este método es muy útil y sencillo para determinar la pendiente y deflexión en las vigas es el METODO DEL AREA DE MOMENTOS, en el intervienen el área del diagrama de momentos y el momento de dicha área. Se comienza, en primer lugar, por los dos teoremas básicos de este método; luego; una vez calculada las áreas y los momentos de estas áreas del diagrama de momentos, se aplica el método de varios tipos de problemas. El método está especialmente indicado en la determinación de la pendiente o de la deflexión en puntos determinados, más que para hallar la ecuación de la elástica. Como en su utilización se ha de tener en cuenta la forma y relaciones geométricas en la elástica, no se pierde el significado físico de lo que se esta calculando.
Este método del área de momentos está sujeto a las mismas limitaciones que el de la doble integración.
En este capitulo usaremos ciertas propiedades geométricas de la curva elástica para determinar la pendiente y la deflexión de la viga en un punto. En lugar de expresar el momento flector como una función M(x) e integrar esta función analíticamente, trazaremos el diagrama que representa la variación de M/EI a lo largo de la viga y evaluaremos ciertas áreas definidas por dicho diagrama y los momentos de las mismas áreas. Este nuevo procedimiento es particularmente útil cuando se requiere obtener las pendientes y las deflexiones solo en ciertos puntos seleccionados de la viga.
.......................................................................................................................................................................................................
MARCO TEORICO:
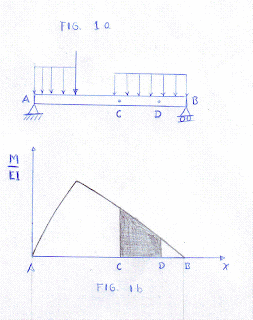
Considérese una viga AB sometida a alguna carga arbitraria (fig. 1a). Se dibuja el diagrama que representa la variación de la cantidad M/EI a lo largo de la viga, que se obtuvo dividiendo el momento flexionante M entre la rigidez de flexión EI (fig. 1b). Se observa que, excepto para distintas escalas en la ordenada, este diagrama será el mismo que el del momento flector si la rigidez a la flexión de la viga es constante.
Al recordar la ecuación y haciendo que dy/dx=θ, se tiene:
Considérese una viga AB sometida a alguna carga arbitraria (fig. 1a). Se dibuja el diagrama que representa la variación de la cantidad M/EI a lo largo de la viga, que se obtuvo dividiendo el momento flexionante M entre la rigidez de flexión EI (fig. 1b). Se observa que, excepto para distintas escalas en la ordenada, este diagrama será el mismo que el del momento flector si la rigidez a la flexión de la viga es constante.
Al recordar la ecuación y haciendo que dy/dx=θ, se tiene:
Al considerar dos puntos arbitrarios C y D en la viga e integrando ambos miembros de la ecuación (1) de C a D, se tiene:
Observase también, en la fig. 1c, que la distancia desde el punto B de la elástica, medida perpendicularmente a la posición inicial de la viga, hasta la tangente trazada a la curva por otro punto cualquiera A, es la suma de los segmentos dt interceptados por las tangentes sucesivas trazadas a la elástica en puntos sucesivos. Cada uno de estos segmentos dt puede considerarse como un marco de radio x y ángulo dθ:
dt = x dθ
De donde

Sustituyendo dθ por su valor en la ecuación (1) se obtiene:
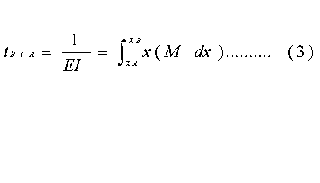
La longitud tB/A se llama desviación de B con respecto a una tangente trazada por A, o bien, desviación tangencial de B respecto de A. El subíndice indica que va desde B hasta la tangente trazada en A. La fig.-3 aclara la diferencia que existe entre la desviación tangencial tB/A de B respecto de A y la desviación tA/B de A con respecto a B. En general, dichas desviaciones son distintas.
................................................................................................................................................................................
La longitud tB/A se llama desviación de B con respecto a una tangente trazada por A, o bien, desviación tangencial de B respecto de A. El subíndice indica que va desde B hasta la tangente trazada en A. La fig.-3 aclara la diferencia que existe entre la desviación tangencial tB/A de B respecto de A y la desviación tA/B de A con respecto a B. En general, dichas desviaciones son distintas.
................................................................................................................................................................................
El significado geométrico de las ecuaciones (2) y (3) conduce a los dos teoremas fundamentales del método del área de momentos. En el diagrama de momentos flexionantes de la fig. 1d, se observa que M dx es el área de elementos diferencial rayado situado a distancia x de la ordenada que pasa por B. Ahora bien, como M dx es la suma de lates elementos, la ecuación (2) se puede escribir en la forma

Esta es la expresión algebraica del teorema I, que se puede anunciar como sigue:
TOREMA I:
La desviación angular, o ángulo entre las tangentes trazadas a la elástica en dos puntos cualesquiera A y B, es igual al producto de 1/EI por el área del diagrama de momentos flexionantes entre estos dos puntos.
La fig. 1d muestra como la expresión x (M dx) que aparece dentro de la integral en la ecuación (3) es el momento del área del elemento rayado con respecto a la ordenada en B. Por tanto, el significado geométrico de la integral x (M dx) es el momento con respecto a la ordenada en B del área de la porción del diagrama de momentos flexionantes comprendida entre A y B. Con ello la expresión algebraica del teorema II es:

Este teorema se anuncia así:
TEOREMA II:
La desviación tangencial de un punto B con respecto a la tangente trazada a la elástica en otro punto cualquiera A, en dirección perpendicular a la inicial de la viga, es igual al producto de 1/EI por el momento con respecto a B del área de la porción del diagrama de momentos entre los dos puntos A y B.
El producto EI se llama rigidez a la flexión. Obsérvese que se supuesto tácitamente E e I permanecían constantes en toda la longitud de la viga que es una cosa muy común. Sin embargo, cuando la rigidez es variable, no puede sacarse EI del signo integral, y hay que conocerla en función de x. Tales variaciones suelen tenerse en cuenta dividiendo entre EI las ordenadas del diagrama de momentos para obtener de esta manera un diagrama de M/EI al que se aplican los dos teoremas, en ves de aplicarlos al diagrama de M.
En los dos teoremas, (área) BA representa el área del diagrama de momentos entre las ordenadas correspondiente a los puntos A y B, XB es el brazo de momentos de esta área con respecto a B. Cuando el área del diagrama de momentos se compone en varias partes (véase la ecuación 4), positivas y negativas, la expresión (área)AB .XB representa el momento del área de todas estas partes. El momento del área se toma siempre con respecto a la ordenada del punto cuya desviación se quiere obtener, por lo que conviene ponerle a X el subíndice correspondientes por ejemplo B, lo que indica que el brezo de momentos se toma hasta esta punto. Observase que este subíndice B es el mismo del numerador del subíndice de t, A/B.
Los convenios de signos siguientes son de gran importancia: La desviación tangencial de un punto cualquiera es positiva si el punto queda por encima de la tangente con respecto a la cual se toma esta desviación, y negativa si queda por debajo de dicha tangente. En la figura 3 se representa las desviaciones positivas y negativas. Recíprocamente una desviación positiva indica que el punto queda por encima de la tangente de referencia. El otro convencionalismo de signos es el que se refiere a las pendientes y se indica en la figura 4. Un valor positivo de la variación de pendiente θAB indica que la tangente en el punto situado a la derecha, B, se obtiene girando en sentido contrario al del reloj la tangente trazada en el punto mas a la izquierda, A; es decir, que para pasar de la tangente en A a la tangente B se gira en sentido contrario al reloj, y viceversa para los valores negativos de θAB.

Esta es la expresión algebraica del teorema I, que se puede anunciar como sigue:
TOREMA I:
La desviación angular, o ángulo entre las tangentes trazadas a la elástica en dos puntos cualesquiera A y B, es igual al producto de 1/EI por el área del diagrama de momentos flexionantes entre estos dos puntos.
La fig. 1d muestra como la expresión x (M dx) que aparece dentro de la integral en la ecuación (3) es el momento del área del elemento rayado con respecto a la ordenada en B. Por tanto, el significado geométrico de la integral x (M dx) es el momento con respecto a la ordenada en B del área de la porción del diagrama de momentos flexionantes comprendida entre A y B. Con ello la expresión algebraica del teorema II es:

Este teorema se anuncia así:
TEOREMA II:
La desviación tangencial de un punto B con respecto a la tangente trazada a la elástica en otro punto cualquiera A, en dirección perpendicular a la inicial de la viga, es igual al producto de 1/EI por el momento con respecto a B del área de la porción del diagrama de momentos entre los dos puntos A y B.
El producto EI se llama rigidez a la flexión. Obsérvese que se supuesto tácitamente E e I permanecían constantes en toda la longitud de la viga que es una cosa muy común. Sin embargo, cuando la rigidez es variable, no puede sacarse EI del signo integral, y hay que conocerla en función de x. Tales variaciones suelen tenerse en cuenta dividiendo entre EI las ordenadas del diagrama de momentos para obtener de esta manera un diagrama de M/EI al que se aplican los dos teoremas, en ves de aplicarlos al diagrama de M.
En los dos teoremas, (área) BA representa el área del diagrama de momentos entre las ordenadas correspondiente a los puntos A y B, XB es el brazo de momentos de esta área con respecto a B. Cuando el área del diagrama de momentos se compone en varias partes (véase la ecuación 4), positivas y negativas, la expresión (área)AB .XB representa el momento del área de todas estas partes. El momento del área se toma siempre con respecto a la ordenada del punto cuya desviación se quiere obtener, por lo que conviene ponerle a X el subíndice correspondientes por ejemplo B, lo que indica que el brezo de momentos se toma hasta esta punto. Observase que este subíndice B es el mismo del numerador del subíndice de t, A/B.
Los convenios de signos siguientes son de gran importancia: La desviación tangencial de un punto cualquiera es positiva si el punto queda por encima de la tangente con respecto a la cual se toma esta desviación, y negativa si queda por debajo de dicha tangente. En la figura 3 se representa las desviaciones positivas y negativas. Recíprocamente una desviación positiva indica que el punto queda por encima de la tangente de referencia. El otro convencionalismo de signos es el que se refiere a las pendientes y se indica en la figura 4. Un valor positivo de la variación de pendiente θAB indica que la tangente en el punto situado a la derecha, B, se obtiene girando en sentido contrario al del reloj la tangente trazada en el punto mas a la izquierda, A; es decir, que para pasar de la tangente en A a la tangente B se gira en sentido contrario al reloj, y viceversa para los valores negativos de θAB.
...................................................................................................................................................................................
GRAFICOS:


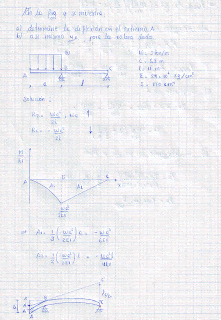






a%3D)

No hay comentarios:
Publicar un comentario