En este capítulo s estudia en detalle las vigas continuas con tres o mas apoyos, dos o mas tramos o claros, y que por lo tanto, disponen de uno o mas apoyos redundantes en los que las reacciones no pueden determinarse por las ecuaciones de la estática. Es posible calcular los valores de estas reacciones hiperestaticas aplicando las condiciones de deformación existentes, de acuerdo con las ecuaciones de deformación del capitulo 6, por ejemplo, deflexión nula en los apoyos cuyas reacciones son desconocidas. Estas condiciones dan las ecuaciones necesarias adicionales a las del equilibrio estático. Sin embargo, es más conveniente considerar como desconocidos o hiperestàticos, los momentos flexionan tes en los apoyos. Una ves determinados estos momentos, que se suelen llamar momentos de continuidad, es sumamente sencillo el calculo de las reacciones, como se vera en la sección 8-5.
Se aplican dos métodos de cálculo de tales momentos. En el primer método se comienza obteniendo una relación de tipo general entre los momentos flexionan tes entre secciones cuales quiera de la viga relación que se llama ecuación de los tres momentos, y que se escribe fácilmente aplicando los teoremas de las áreas de momentos. Las aplicaciones de esta ecuación son numerosas; con ella pueden resolverse todos los problemas de los capítulos 6-7. Así como determinar las deformaciones y reacciones redundantes en cualquier tipo de vigas en particular en las vigas continuas. En muchos casos se puede aplicar junto con los teoremas de las áreas de momentos o con el método de la doble integración, como se tendrá ocasión de ver y aplicar.
El segundo método es el método de la distribución de momentos, que se aplica y desarrolla en la sección 8-8. Este método es independiente del anterior, aunque la determinación del diagrama de fuerza cortante y de las reacciones sea común para ambos. Para aplicar este método se empieza suponiendo que cada tramo o claro esta perfectamente empotrado en sus extremos y se determinan los momentos de empotramiento perfecto. En la mayoría de los casos, las cargas sobre cada tramo son de los tipos que aparecen en la tabla 7-2 o combinaciones de estos tipos. En estas condiciones, los momentos de empotramiento perfecto (MEP) se calculan por superposición o se toman directamente de la tabla. Para tipos más complejos de cargas, y si no se dispone de una tabla que tenga más casos, es preferible emplear el primer método.
GENERALIDADES
OBJETIVOS:
Se aplica para calcular reacciones, diagramas de momentos flectores, fuerzas cortantes y deformaciones.
JUSTIFICACION:
Se aplica la ecuación de los tres momentos a la determinación de los momentos de continuidad en los apoyos de una viga continua. En secciones siguientes se muestra la determinación de la las reacciones a partir de los momentos hallados. Por ultimo, se indica un momento muy rápido para trazar los diagramas de fuerza cortante y momento flexionante.
LIMITACIONES:
Este teorema se aplica generalmente para vigas hiperéstaticas continuas de dos a mas tramos.
MARCO TEORICO
FORMA GENERALIZADA DE LA ECUACIÒN DE LOS TRES MOMENTOS
En la figura 8-1a se representa parte de una viga sometida a una carga cualquiera y sometida a una carga arbitraria. Cortemos la viga por tres puntos cualesquiera 1, 2, y 3 y sustituyamos el efecto de las cargas y fuerzas a la derecha o a la izquierda de cada sección de corte por la fuerza cortante y momentos flexionantes (SEC. 4-3). En la figura 8-b se representa los diagramas de cuerpo libre correspondientes a los tramos a segmentos de viga entre las secciones 1 y 2 y entre las secciones 2 y 3 que, en adelante, se llamaran tramo 1 y tramo 2, respectivamente. Las longitudes de los tramos son L1 y L2 y los momentos flexionantes en 1, 2, 3 son M1 M2 y M3 que, según la sección 4-3 y tal como están dibujado, son los tres positivos, de donde el sentido de las flechas es el indicado (del reloj, a la izquierda, y contrario al del reloj, a la derecha del tramo). Las fuerzas cortantes en estos puntos son V1 , V-2 (justo a la izquierda del punto 2), V2 (justo a la derecha del punto 2) y V-3 (justo a la derecha del punto 3 ). Las fuerzas V-2 y V2 no tienes que ser iguales en general, pues sus valores dependen naturalmente de lo que haya en el punto 2. De acuerdo con la sección 4-2, y puesto que en el extremó izquierdo se ha de poner la fuerza cortante real y en el derecho la resistente tal como esta dibujadas las flechas V1 y V2 y son fuerzas cortantes positivas, mientras que V-2 y V-3 son fuerzas cortantes negativas.
El procedimiento estudiado en la sección 7-5 proporciona el medio para transformar cada uno de estos tramos en una viga simplemente apoyada con dos estados de cargas; por un lado la carga real del tramo y por otro lado los pares aplicados en sus extremos. En las figuras 8-2a y 8-2b se representan estos dos estados de carga, para los dos tramos cuya superposición reproduce el estado supuesto en los diagramas de cuerpo libre de la figura 8-1b. Las fuerzas cortantes en los extremos de cada tramo será, para el extremo izquierdo, igual a la suma de las reacciones de los dos estados, y para el extremo derecho igual numéricamente pero de signo contrario. Las reacciones del primer estado (cargas reales sobre el tramo, que se considera apoyado), se calcula por las ecuaciones de equilibrio estático, y lo mismo para las del segundo, que forman un par de reacciones iguales y opuestas R’ que equilibran el par M1 - M2 por ejemplo.
En estas condiciones, el diagrama de momentos flexionantes en cada tramo de la viga se resuelve por partes en el diagrama que produce cargas existentes sobre el tramo suponiendo que el tramo estuviera simplemente apoyado en sus extremos mas el diagrama trapezoidal producidos por los pares aplicados en los extremos de la misma viga, tal como se indica perfectamente en las figuras 8-2c y 8-2d.
En la figura 8-3 aparece representada la elástica de la viga sumamente exagerada, para ver con mas claridad las relaciones geométricas que se van a utilizar. Obsérvese que los puntos 1, 2 y 3 están precisamente en la elástica.
La tangente trazada a la elástica en el punto 2 determina las desviaciones tangenciales t1/2 y t3/2 de los puntos 1 y 3, respectivamente y la recta trazada por 2 paralela a la posición inicial de la viga, que por conveniencia se supone horizontal, determina la altura de los puntos 1 y 3 con respecto al 2, alturas q son h1 y h3. Los triángulos sombreados en la figura tienen por base L1 y L2 y por altura (h1 - t1/2) y (t3/2 - h3), y por ser semejantes resulta obvio que:
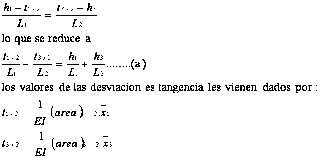
Siendo (área) 1-2. X1 el momento de área del diagrama de momentos flexionantes entre los puntos1 y 2 respecto del punto 1. Como se estableció previamente, el diagrama de momentos flexionantes se había descompuesto en el área A1 (fig. 8-2c) y las dos áreas triangulares en las que se descompone el área trapezoidal producida por los dos pares extremos (fig. 8-2d). Los mismo pasa con (área)3-2. X3, que es el momento del área de momentos entre los puntos 2 y 3 respecto del punto 3, y que se descomponen de forma similar.
En estas condiciones ya se puede expresar el valor de la desviación de l punto 1 con respecto a la tangente en 2 viene dada por:


En esta ecuación expresa una relación general entre los momentos flexionantes en tres puntos cualesquiera de la viga, razón por la cual se llama ecuación de los tres momentos.
Si los puntos 1, 2 y 3 están al mismo nivel en la viga deformada las alturas h1 y h3 de la figura 8-3 se anulan, y lo mismo ocurre en el mismo miembro de la ecuación (8-1). Esta suele ser la condición normal de aplicación de la ecuación de los tres momentos a la determinación de los momentos de continuidad. Los tres puntos que se escogen para aplicar la ecuación a una viga continua son tres apoyos, que suelen suponer rígidos o situados a la misma altura y entonces mediante la ecuación se determinan los momentos en dichos apoyos.
Si se quiere aplicar la ecuación de los tres momentos para calcular las ordenadas de la elástica, se consideran dos de los puntos sobre dos apoyos y el tercero en el punto en el donde se quiere hallar la ordenada. En este caso, evidentemente, es necesario calcular de antemano los valores de los momentos en los tres puntos. En la sección 8-7 se vera con mas detalle esta forma de aplicación de la ecuación de los tres momentos.
REGLA DE SIGNOS:
En la deducción de la ecuación (8-1) se ha hecho la hipótesis de que los momentos flexionantes en los tres puntos son positivos y que los puntos 1 y 3 están situados por encima del punto 2. Si el momento flexionante en cualquiera de los puntos es negativo habrá que considerarlo como signo menos al sustituir su valor en la ecuación. Recíprocamente, si al resolver la ecuación sale un valor negativo a cualquiera de los momentos, es que en realidad es negativo. Las alturas h1 y h3 son positivas si los puntos 1 y 3 quedan por encima de 2 y son negativos, o se obtendrán con signo menos, si el punto 1 o el 3 esta por debajo del punto 2.























2 comentarios:
... de que libro es la tabla con las vigas continuas y los valores de Aa/L
Casino of the Sky Hotel & Casino
This casino, 춘천 출장샵 located in The Sky Casino of Sky, has the very best selection 군산 출장안마 of table games and live 제천 출장안마 entertainment, 광명 출장샵 big name casino 경상북도 출장샵 games and live
Publicar un comentario